前言/Abstract
作者是瑞典医学院的 Sten Linnarsson 和哈佛药学院的 Peter Kharchenko 。
这篇文章主要是提出了一个 RNA velocity 的概念。通过标准单细胞测序数据测量得到mRNA剪切前后的比例来估计RNA丰度随时间的变化。作者认为这种变化代表了细胞状态的改变,是一种动态的对单细胞状态的观测。而寻常的RNA丰度分析手段并不能展现出一个动态的细胞状态变化的过程。
进一步,这个指标可以用于预测每个细胞当前状态的下一个状态(以小时为基本时间尺度)。
作者在神经嵴细胞系 (Neural crest lineage) 中验证了这一指标的准确性,在文章中展示了具体应用方式,重建了小鼠海马体 (mouse hippocampus) 的分化树 (branching lineage tree), 测试了人类胚胎脑部的RNA变化。
作者希望这个指标可以用于协助分析和揭示人类细胞的谱系发育和细胞内的动态变化。
主要亮点
- 对原本是静态的测序数据进行了重新诠释让它能展现出一种动态的信息
大概原理
太长不看版
工具输入raw reads和聚类地图坐标,输出是带方向的地图
步骤
- 针对每个细胞及每个基因数出 spliced reads & unspliced reads
- 使用model I 每个基因所有的细胞的spliced reads$\upsilon$和 unspliced reads$s$ 估计出降解率 $\gamma$ for $\upsilon=\gamma s$
- 之后对每个细胞的各个基因的unspliced reads使用$\gamma$计算 “下一个时刻(概念化的短时间步长)” 成熟程度,认为这是这个细胞下一步的状态
- 每个细胞的下一步状态和其他所有细胞当前状态作correlation,作为向量模长,向量方向即细胞指向其他细胞的方向
- 将每个细胞算得的所有向量线性相加,即可得到最终这个细胞在聚类地图上下一步的走向
Some notes
这个方法的指向必须是已经测得的细胞,所以并不能揭示潜在路径
这个方法主要就是在tracing的时候提示已知细胞群里最有可能的发育方向
因为使用了 unspliced reads 因此还是从数据中又多回收了一部分信息量的。
详细一点的原理
主要是对“骑墙”reads进行分类和统计。
跳过整个intron,横跨exon/exon边界的reads,作者认为来自于经过剪切的成熟RNA。
跨过了exon/intron边界的reads是来自于没有经过剪切的mRNA。
完全在exon中的reads既可以来自成熟mRNA也可以来自于未剪切的mRNA,
而完全在intron中的reads作者认为可能来自于非特异背景(噪音吧就)或者是潜在的其他transcripts
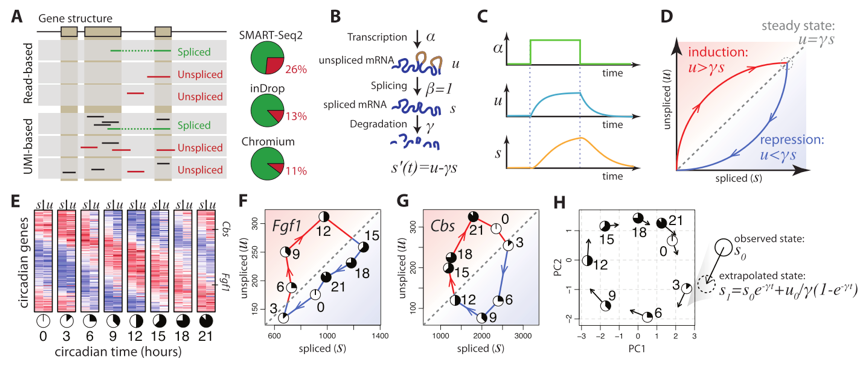
中间作者介绍了一下关于几个常见测序protocol捕获mRNA前体能力的论证。
(对于mRNA和mRNA前体的捕获能力可能存在bias,不同方法的捕获能力也有差距, Fig1A)
具体用来测算所谓“剪切速度”的模型十分简单,本质上是一个动力学平衡公式,如同Fig1B所示,
转录速率 $\alpha$, 得到mRNA前体量 $\upsilon$, Splicing rate $\beta$, Spliced mRNA $s$, Degradation rate $\gamma$
当处于稳态时,显然有
$$\begin{equation}
\upsilon=\gamma s
\end{equation}$$
转录速率 $\alpha$ 的升高或降低都会引起u的变化从而形成新的稳态平衡,因此作者希望通过跟踪$u$和$s$来预测未来mRNA变化量。
通过测量不同mRNA的这种剪切-成熟平衡,可以对每个细胞估计出一个高维向量,由于这些向量揭示的实质上是一个动态变化过程,因此作者希望用这种方法可以预测细胞未来的状态。
从Fig1 EFG可以看到,通过对sliced/unsliced的reads进行定量,细胞周期相关的基因呈现出一种周期性的变化。
作者发现和周期相关的基因都能根据斜率$\gamma$和unsliced reads $s$进行定量预先观察到上下调的行为。
1H是作者把上述公式解了出来,然后推测细胞周期下一个state的位置,plot到pc图上,主要是想看看能不能用这个方法推测细胞state。
但具体怎么解的公式、计算的slope还需要进一步深挖细节
数据
小鼠嗜铬细胞的单细胞mRNA-Seq(SMART-Seq2)数据。在发育过程中,大量的嗜铬细胞(肾上腺髓质的神经分泌性细胞),从神经脊的Schwann 细胞前体分化而来。
这条路径可以很方便通过追踪细胞系的分化路径来对他们的方法进行测试。
结果
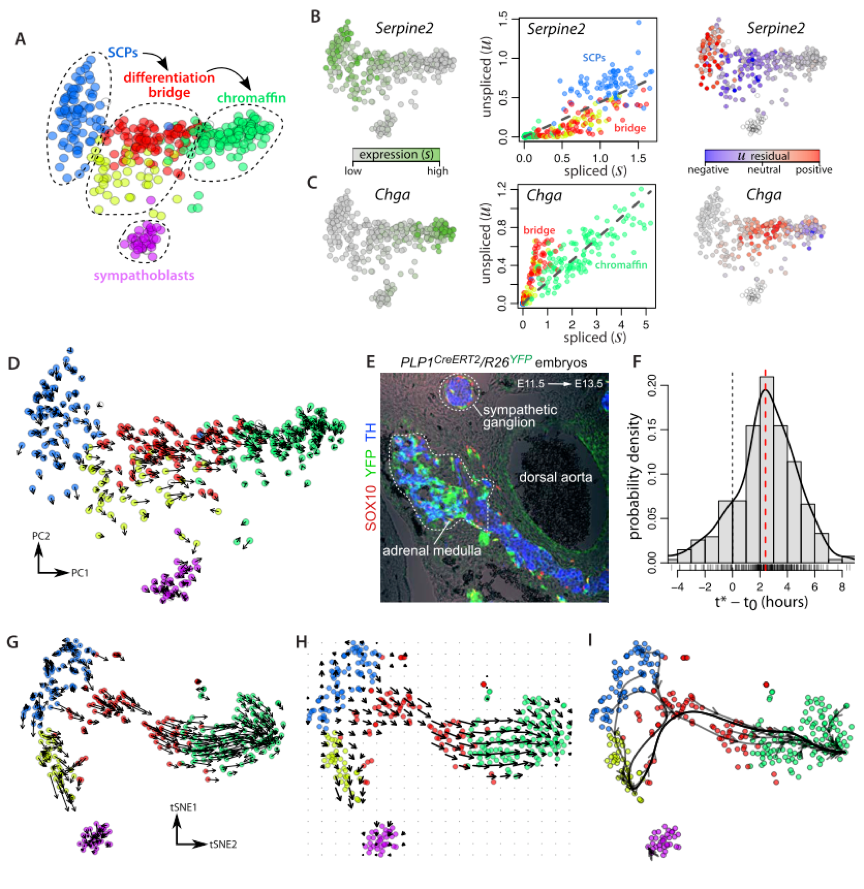
Fig2展示了这个数据集用作者方法得到的预测结果。值得注意的是,每个细胞的数据在聚类后用最相似的k=5个细胞pool了一下。
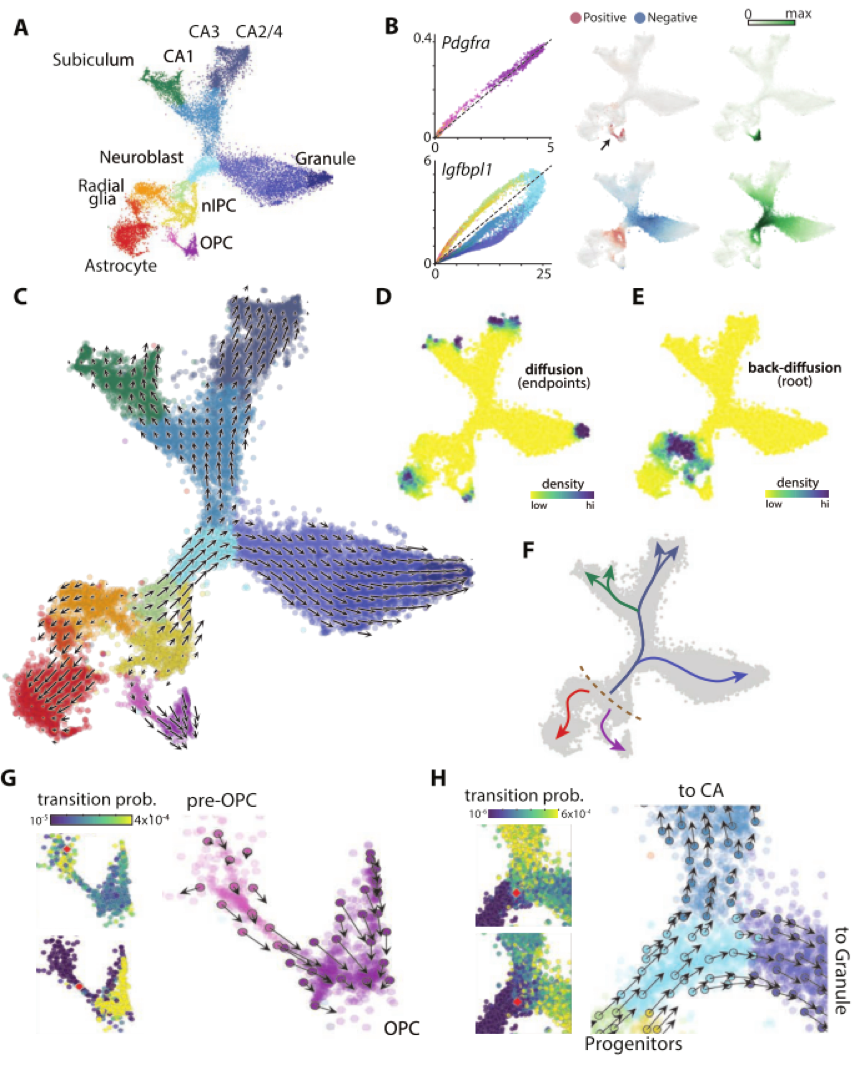
未完待续
详细方法
RNA velocity 的理论描述
基于Fig1的图形

对于任意时间点的:
unspliced mRNA molecules $u$
spliced mRNA molecules $s$
$$\begin{align}
\frac{du}{dt} &= \alpha(t) - \beta(t)u(t) \\
\frac{ds}{dt} &= \beta(t)u(t) - \gamma(t)s(t)
\end{align}$$
Here, $\alpha(t)$ is the time-dependent rate of transcription, $\beta(t)$ is the rate of splicing, $\gamma(t)$ is the rate of degradation. Under an assumption of constant (time-independent) rates $\alpha(t)$ = $\alpha$,
$\gamma(t)$ = $\gamma$, and setting $\beta(t)$ = 1 (i.e. measuring all rates in units of the splicing rate)
The rate equation simplify to:
$$\begin{align}
\frac{du}{dt} &= \alpha - u(t) \\
\frac{ds}{dt} &= u(t) - \gamma s(t)
\end{align}$$
The complete solution to these equation is:
$$\begin{align}
u(t) &= \alpha(1-\it{e}^{-t}) + u_0\it{e}^{-t} \\
s(t) &= \frac{\it{e}^{-t(1_\gamma)} \left[\it{e}^{t(1+\gamma)}\alpha(\gamma -1) + \it{e}^{t\gamma}(u_0 - \alpha)\gamma + \it{e}{t}\left(\alpha - \gamma(s_0 + u_0 + s_0\gamma)\right) \right]}{\gamma(\gamma - 1)}
\end{align}$$
若群体处于平衡态(steady-state),那么有$\frac{ds}{dt} = 0$ 则有
$$\begin{equation}
\gamma = \frac{u}{s}
\end{equation}$$
但如果群体不处于终末分化的状态(也就是平衡态),那么这个是不成立的,对于那些快速变化的分化中细胞,$\gamma$ 需要通过下述方法来估计。
最大的问题是,我们并不知道$\alpha$也就是每个转录本的转录效率,也很难估计。这就很难得到我们想要的未来的$s(t)$。所以我们通过下述两个模型,不是估计$\alpha$而是直接估计$s(t)$
Model I. Constant velocity assumption:
这个模型假设剪切效率不变即$\frac{ds}{dt}=v$。此时推断变得容易因为$s(t) = s_0 + vt$。
在实际使用中,短时间内效果还行,但是对于更长时间段的变化的推断,如果$v<0$(i.e. 下调基因), 那么$s(t)$可能为负。
所以需要把负值都变为0
Model II. Constant unspliced molecules assumption:
另外,我们还可以假设未剪切的分子数保持不变,比如$u(t) = u_0$, 公式可以化简为
$$\begin{equation}
\frac{ds}{dt}=u_0 - \gamma s(t)
\end{equation}$$
方程解变形为
$$\begin{equation}
s(t)=s_0\it{e}^{-\gamma t} + \frac{u_0}{\gamma}(1-\it{e}^{\gamma t})
\end{equation}$$
假设基因独立的情况下,一个单细胞的总体RNAvelocity就是一个由各个基因组成的多维向量。
估计 RNA velocity
对于每个基因,均一化矫正的降解率$\gamma$都用最小二乘法拟合这个线性模型$u ~{} \gamma * s + o$得到。其中$u = \frac{U}{N}$和$s = \frac{S}{N}$, N代表总reads counts, U代表unspliced reads counts, S代表splicaed reads counts。
$o$是一个常数项,代表的是可能受到未注释的转录本影响的内含子counts基线。也有多种方法进行估计。
在Model I下,velocity $v = u - \gamma s - o$,一个给定细胞下的给定基因预测下个时间点的counts被定义为$s_t = max(0, s_0 + vt)$。t是一个时间单位,在这个尺度下总RNAcount不应该有太大变化。
Model II下则 $\Delta s(t) = \left(\frac{\hat{x}}{\gamma} - s\right)(1-e^{-\gamma t})$,其中$\hat{u} = \frac{\max(0, U-o*N)}{N}$,是一个矫正过的unspliced counts。
并且默认$t=1$,预测的counts $S_t = \max(0, S + \Delta s(t) N)$,S是一个未经过矫正的spliced counts。均一化矫正的推测的counts $s_t = \frac{S_t}{\hat{N}}$ , $\hat{N}$是一个推测的细胞总counts数 $\hat{N} = N+S_t - S$
Cell nearest neighbor(kNN) pooling
为了增加$\gamma$的估计准确度,所以作者把几个临近相似的细胞pool到一起进行估计。针对smart-seq2的测序数据,作者用Person correlation找到 k个最近的细胞,而10X 和inDrop数据使用PCA的欧氏距离找的。找到以后把它们的$S,U$ counts加起来作为新的数据点。
velocity 可视化
未完待续
版权声明: 本博客所有文章除特别声明外,均采用CC BY-NC-SA 3.0 CN许可协议。转载请注明出处!