Note: Isoform-level gene expression patterns in single-cell RNA-sequencing data

发表于 | 分类于 |

Abstract

这篇文章早在2016年就在bioRxiv上online了，但是一直到今年才在bioinformatics上发出来。
文章主要贡献是通过混合模型描述了单细胞的isoform的表达pattern。算是比较少的对单细胞RNAseq isoform level进行描述。

在这篇文章里作者介绍了一种方法，ISOform-Patterns(ISOP), 来分析并且分类单细胞的isoform基因表达量数据。
主要提出了同一个基因下不同isoform的6种表达模式。
为了得到系统性的对单细胞isoform表达 pattern 进行分类， 作者在在一个乳腺癌细胞系(MDA-MB-231; N=327 cells)上进行了尝试并且在其他三个数据集上进行了重复(?)。
作者随后评估了单细胞的随机性对这些pattern产生所造成的影响， 并且阐释了ISOP如何能够用来分析差异性的isoform pattern。
最后作者用一个模拟数据集测试了ISOP方法。

作者信息

暂无

Introduction

pass

Method

Data preprocessing

  • Dataset: triple- negative breast cancer cell line MDA-MB-231 single cell RNA-Seq data
  • hg19 Tophat + bowtie + Cufflinks
  • Exclude isoforms expressed(reads counts > 3) in less than 1% samples
  • 21728 isoforms, of which 13863 isoforms from 4929 genes that are multiple-isoform genes
  • 326 cells, of which 162 were metformin treated.

pattern of isoform expression

使用高斯混合模型对于一个细胞$i$表达的一个基因$j$的一对isoforms$\{a, b\}$而言，log变换后的表达量$\Delta_{i,j,a,b}$ $\eqref{eq1}$ 进行拟合$\eqref{eq2}, \eqref{eq3}$。
$y_{i,j,a}$ 和 $y_{i,j,b}$ 代表的是isoform $a$和$b$ 在细胞$i$里的log表达量。
参数$w_k$是混合的$k$ component权重，$K$是总component数。作者把$K$限制到 $\leq 3$, $N$ cells in total。

$\eqref{eq2}, \eqref{eq3}$ 的gene $j$ 和 cell $i$编号都省略。

$$\begin{align}
\Delta_{i,j,a,b} &= y_{i,j,a} - y_{i,j,b} \label{eq1} \\
f(\Delta_{a,b}) &= \sum_{k=1}^K{w_kN(\Delta_{a,b}|\mu_k,\sigma_k)} \label{eq2} \\
\sum_{k=1}^Kw_k &= 1 \label{eq3}
\end{align}$$

Component数量基于Akaike infromation criterion scores，并且要求最小的权重$w_k > 0.025$ 以及 所有component的标准偏差 (standard deviation) $> 0.01$。 (histogram based method implemented in the OCplus, here the bins number are set to the square root of number of cells )

Test for non-randomeness of isoform-pair distributions

为了测试一个isoform pairs分布随机产生的可能性
对于一对isoform $\{a,b\}$, 随机打乱$a,b$标签，然后计算 $\Delta_{a,b,perm}$，并进行10000次重复。

作者应该是首先假设$\Delta_{a,b}$服从卡方分布，

计算期望$E(\Delta_{a,b,perm})$
Null-distribution 是基于 kth permuted isoform pair $\Delta_{a,b,perm}(k)$ 和 $E(\Delta_{a,b,perm})$ 之间做 $\chi^2$ goodness-of-fit test 的 （$\chi^2$统计量）的分布
Observed test statistic 就是 原始的 $\Delta_{a,b}$ 和 $E(\Delta_{a,b,perm})$ 的 $\chi^2$ goodness-of-fit test 的 $\chi^2$ 统计量。

把Observed test statistic 和已有的Null distribution进行比较就可以得到一个 p-value，代表的就是原有分布是由随机性产生的可能性

DP analysis

Treatment effect(metformin exposure) associated with the probability of cells of being clustered into a particular mixture model component in the isoform pattern models.对这个进行测试能够阐述是否一些实验条件能够影响isoform pair的表达pattern。

a permutation test for permuting cluster label which is based on mixture model.

  • Permute cluster labels, which is assigned by fitted mixture model.
  • Null-distribution: $\chi^2$ statistics of $\chi^2$ test between cluster labels and the permuted label.
  • Test statistic: $\chi^2$ statistics of $\chi^2$ test between cluster labels and the true group label(condition)

Results

Based on the mixture model to medel isoform expression difference ($\Delta_{a,b}$) on a log scale.

Principal patterns

  • I-pattern: 单component。 但如果均值不等于零，那么说明其中一个isoform是被几乎所有细胞偏好的
  • II-pattern: 是I-pattern的扩展， 双component， 说明有一部分细胞的某种isoform是不表达或一部分细胞里的两种isoform表达量分布没有明显差异。这种pattern说明了一部分细胞对isoform的偏好
  • V-pattern: 双component，说明isoform之一是unimodal而另一个bimodal。 因此这个pattern展现的是其中一个bimodal distributed isoform在不同细胞群体中的偏好
  • VI-pattern: 三component， 和V-pattern区别在于多了一个均值在0附近的component， 这个component说明两个isoform有一部分细胞的表达量是相近的
  • X-pattern: 三component， 两个表明互斥关系，第三个component（绿）标明zero-inflation。这是一种很特别的细胞间差异。
  • XI-pattern: 三component， X-pattern的扩展，有一部分细胞同时表达两个isoform， 因此互斥关系只存在于一部分细胞中。

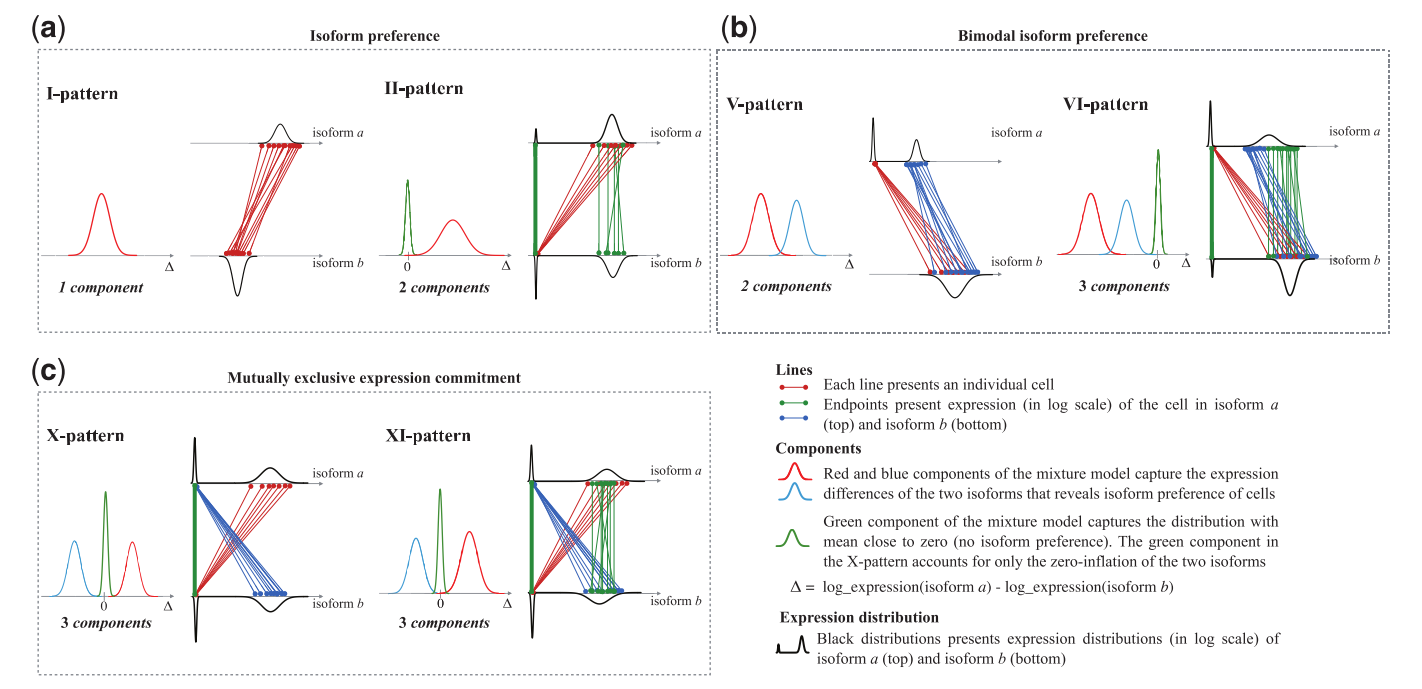
Classification and observed frequencies of isoform patterns

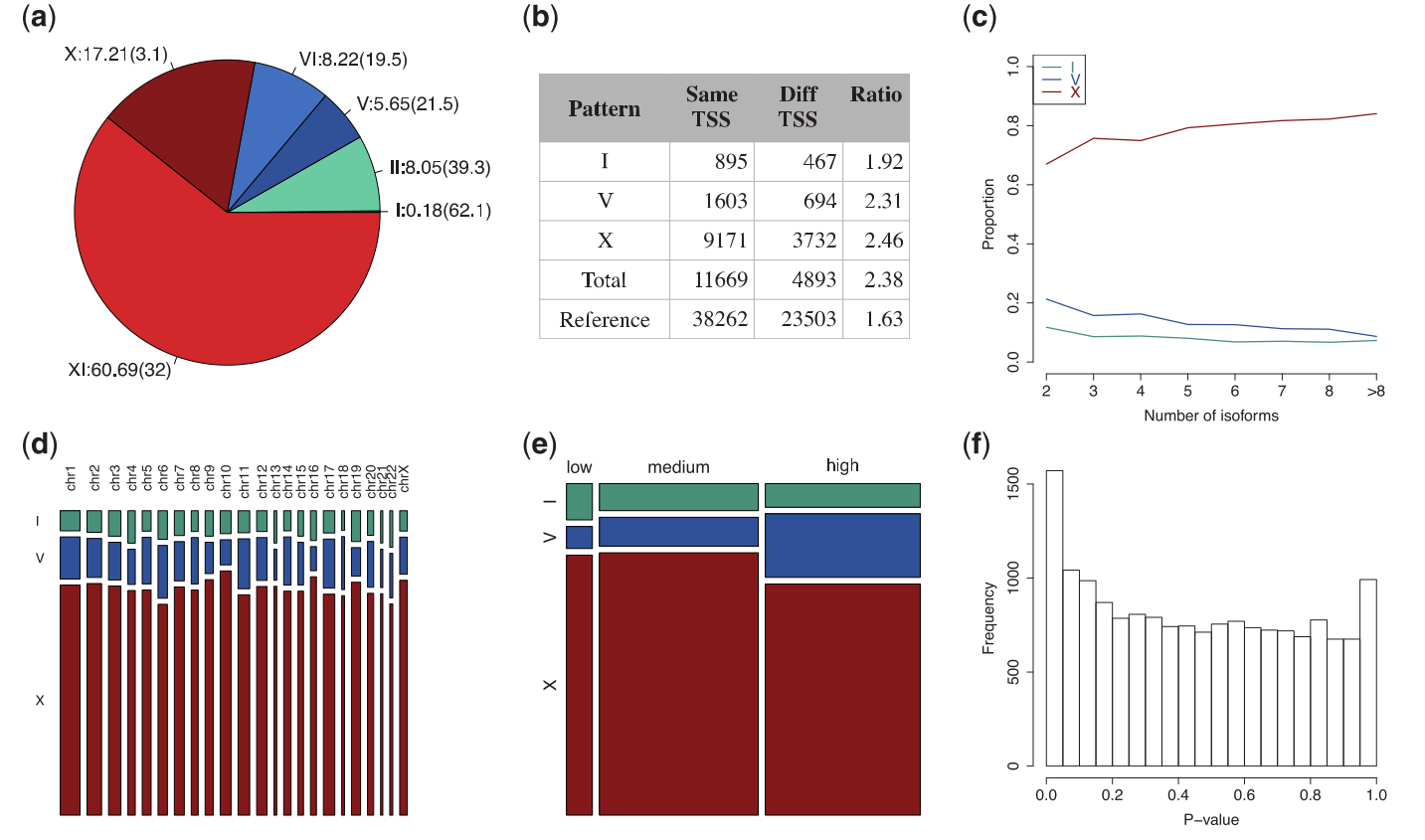
总共4929个多isoform基因和13863个isoform，总共检测到16562个isoform-pairs。比例如fig2a所示。 小括号里是经过permutation test以后差异显著的pairs百分比。显著百分比前三位是I/II/XI。

A是找到的各个比例，小括号里是显著的比例
BCDE是尝试寻找isoformpattern和TSS、isoform数量，染色体位置和平均表达量的关系
把IVX和它们的extent合了起来一起做。

Fig2:
A是找到的各个比例，小括号里是显著的比例
BCDE是尝试寻找isoformpattern和TSS、isoform数量，染色体位置和平均表达量的关系
把IVX和它们的extent合了起来一起做。
几个描述性的结果吧
B主要就是，起始于同一个TSS的比起始于不同TSS要多2倍左右
C就是isoform更多更容易出现Xpattern，
D没什么差异
E average gene expression distribution < 1 quantile| 1-3 quartile | >3 quartile 更多的isoform pairs处于中表达量和高表达量
F association test, suggesting an enrichment of low P-values

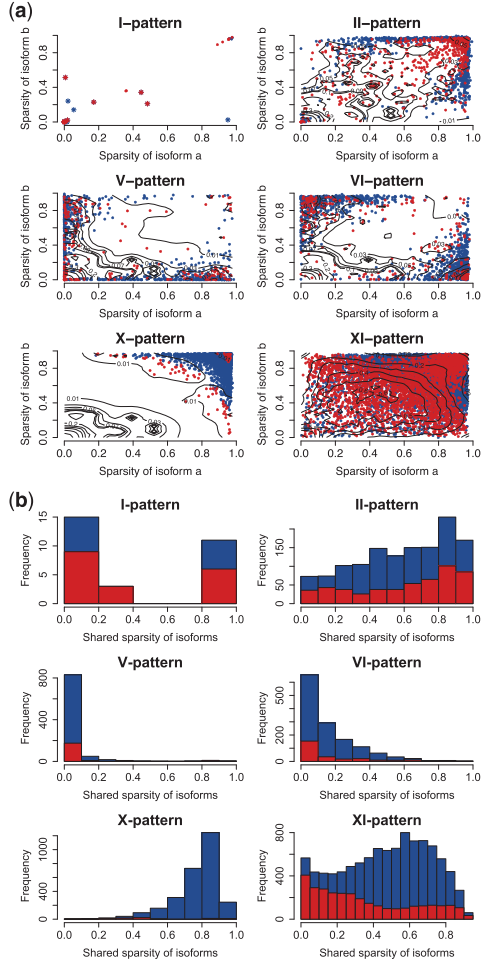
紧接着作者评估了稀疏性对isoform的影响，
sparsity的定义是，不表达细胞所占总细胞量的比例，所以低稀疏性的isoform表达它的细胞越多。反之则少。
fig3a 里X-pattern显示的稀疏性都极高，意味着这个pattern多有可能是由于稀疏性高造成的。

版权声明： 本博客所有文章除特别声明外，均采用CC BY-NC-SA 3.0 CN许可协议。转载请注明出处！